→
큐(Queue) 란?
- 선입선출(FIFO, First In First Out) 형식을 갖는 자료구조 → 먼저 들어간 입력이 먼저 나옴
2024.03.12 - [Algorithm/개념] - [자료구조] 큐(Queue)
[자료구조] 큐(Queue)
큐(Queue) 란? 선입선출(FIFO, First In First Out) 형식을 갖는 자료구조 → 먼저 들어간 입력이 먼저 나옴 종류 선형 큐(Linear Queue) 일반적인 리스트 형태를 갖으며, 선입선출 형식을 갖음 원형 큐(Circular
l1m3kun.tistory.com
힙(Heap) ?
- 우선순위 큐를 위해 고안된 완전 이진 트리 형태의 자료구조

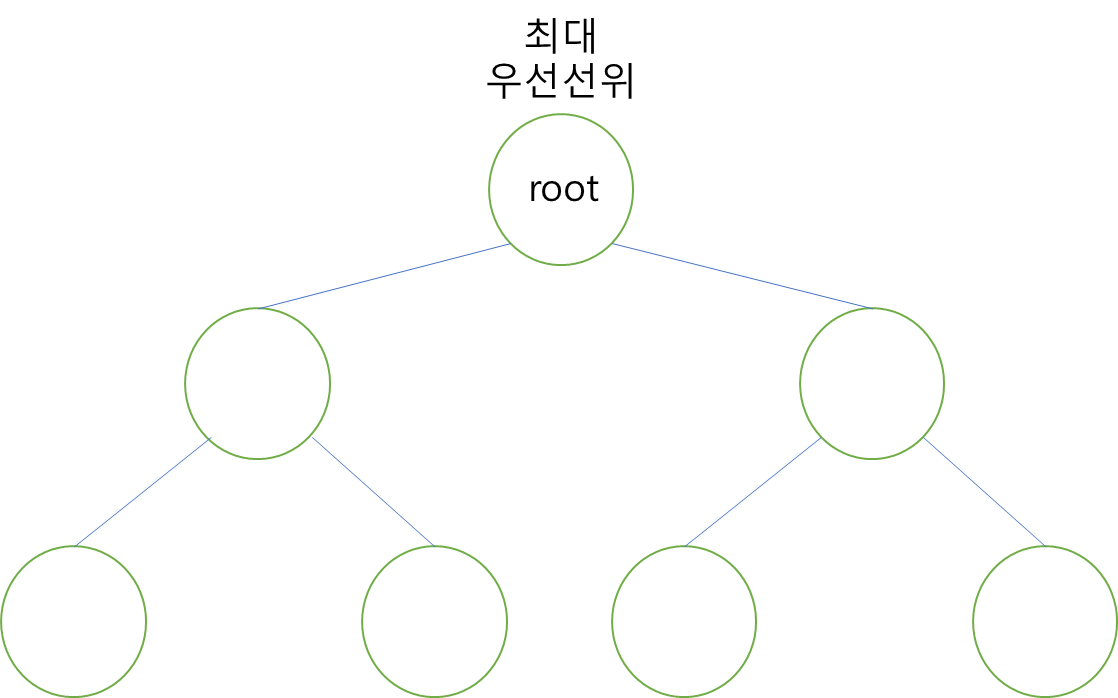
우선순위 큐
- 최대 우선순위를 부모 노드에서 자식 노드로 갈 수록 우선순위가 내려간다. → Root 노드가 최대 우선순위를 갖는다.

- 단, 같은 level의 자식 노드 사이에선 우선순위가 상관없다. → 내 자식노드가 내 level의 노드보다 높은 우선순위를 갖을 수 있다.

구현(최소 힙 기준)
- 트리 생성
last = -1
tree = [0] * N- 요소 삽입
- 마지막 위치에 요소를 삽입한 후, 부모 노드와 비교하며 힙 정렬
length += 1
tree[length-1] = num
node = length-1
while node >= 0:
if node % 2:
parent = node // 2
else:
parent = node // 2 - 1
if tree[parent] > tree[node]:
tree[parent], tree[node] = tree[node], tree[parent]
node = parent
else:
break- 요소 삭제
- Root 위치(최대 우선순위)를 빼낸 후, 가장 끝 노드의 값을 Root 위치에 넣음
- Root부터 비교하며 힙 재정렬
tree[0], tree[length] = tree[length], 0
length -= 1
node = 0
while node < length:
left, right = 2*node+1, 2*node+2
if node >= length:
break
if left >= length and right >= length:
node += 1
elif left >= length:
if tree[node] > tree[right]:
tree[node], tree[right] = tree[right], tree[node]
node = right
elif right >= length:
if tree[node] > tree[left]:
tree[node], tree[left] = tree[left], tree[node]
node = left
else:
if tree[left] > tree[right]:
if tree[node] > tree[left]:
tree[node], tree[left] = tree[left], tree[node]
node = left
else:
if tree[node] > tree[right]:
tree[node], tree[right] = tree[right], tree[node]
node = right
# node가 변화가 없으면 멈춤
if node != right and node != left:
break
Code
class PriorityQueue:
def __init__(self, N:int) -> None:
# 전체 길이를 미리 선정하여 heap list를 생성
# 길이를 미리 저장
self.tree = [0] * (2*N+2)
self.length = 0
# 힙 소트(시작 노드를 입력받음)
# 시작 노드 0 -> root에서 아래로 내려감
# 시작 노드 0이 아닌 다른 인덱스 -> 인덱스에서 위로 올라감
def heap_sort(self, node:int) -> None:
# 시작노드가 root 노드 일 때 -> 아래로 내려감
if node == 0:
while node < self.length:
left, right = 2*node+1, 2*node+2
# 길이를 넘어가면 트리에서 벗어남(leaf 노드가 0임)
if node >= self.length:
break
if left >= self.length and right >= self.length:
node += 1
# leaf 노드에서 하나만 넘어가는 경우(leaf 노드가 없는 경우)
elif left >= self.length: # 왼쪽 leaf 노드 0
# 부모 노드가 더 크면 바꿈
if tree[node] > tree[right]:
tree[node], tree[right] = tree[right], tree[node]
node = right # 다음 탐색 확인
elif right >= self.length: # 오른쪽 leaf 노드 0
if tree[node] > tree[left]:
tree[node], tree[left] = tree[left], tree[node]
node = left
else:
# 모두 범위 내의 경우(leaf 노드가 둘 다 있는 경우)
# 왼쪽 leaf 노드와 오른쪽 leaf 노드를 비교
# 더 작은 쪽 leaf 노드와 root 노드 비교 -> root 노드가 더 크다면 교환
if tree[left] > tree[right]:
if tree[node] > tree[left]:
tree[node], tree[left] = tree[left], tree[node]
node = left
else:
if tree[node] > tree[right]:
tree[node], tree[right] = tree[right], tree[node]
node = right
# 다음 노드를 탐색하지 더 이상 않아도 되는 경우 break
if node != left and node != right:
break
else: # 시작 노드가 0이 아닌 경우 -> leaf 노드에서 root노드 쪽으로 탐색
while node > 0:
# 인덱스가 leaf 노드 기준 왼쪽(홀수), 오른쪽(짝수)
# parent node(N) -> left leaf node (2*N+1) / right leaf node (2*N + 2)
if node % 2: # left leaf node (2*N+1) -> (2*N+1)//2 = N
parent = node // 2
else: # right leaf node (2*N+2) -> (2*N+2) //2 -1 = N
parent = node // 2 - 1
# root 노드와 비교하여 교환할 여지가 있으면 교환하여 탐색
if tree[parent] > tree[node]:
tree[parent], tree[node] = tree[node], tree[parent]
node = parent
else: # 교환할 필요 없으면 더 이상 탐색 X
break
return
# 힙 푸시
def push_num(self, num:int) -> None:
# 마지막 노드에 추가하여 힙 소트(leaf -> root)
self.tree[self.length] = num
self.heap_sort(self.length)
self.length += 1
return
# 힙 팝
def pop_num(self) -> int:
# root 노드를 제거한 후, 마지막 leaf 노드를 root 노드에 넣어 힙 소트(root -> leaf)
if self.length == 0:
return 0
root = self.tree[0]
self.tree[0], self.tree[self.length-1] = self.tree[self.length-1], 0
self.length -= 1
self.heap_sort(0)
return root예제 문제
https://www.acmicpc.net/problem/11279
11279번: 최대 힙
첫째 줄에 연산의 개수 N(1 ≤ N ≤ 100,000)이 주어진다. 다음 N개의 줄에는 연산에 대한 정보를 나타내는 정수 x가 주어진다. 만약 x가 자연수라면 배열에 x라는 값을 넣는(추가하는) 연산이고, x가 0
www.acmicpc.net
https://www.acmicpc.net/problem/1927
1927번: 최소 힙
첫째 줄에 연산의 개수 N(1 ≤ N ≤ 100,000)이 주어진다. 다음 N개의 줄에는 연산에 대한 정보를 나타내는 정수 x가 주어진다. 만약 x가 자연수라면 배열에 x라는 값을 넣는(추가하는) 연산이고, x가 0
www.acmicpc.net
응용 문제
https://www.acmicpc.net/problem/11286
11286번: 절댓값 힙
첫째 줄에 연산의 개수 N(1≤N≤100,000)이 주어진다. 다음 N개의 줄에는 연산에 대한 정보를 나타내는 정수 x가 주어진다. 만약 x가 0이 아니라면 배열에 x라는 값을 넣는(추가하는) 연산이고, x가 0
www.acmicpc.net
문제풀이
2024.03.12 - [Algorithm/BaekJoon Review] - 11286. 절댓값 힙
11286. 절댓값 힙
https://www.acmicpc.net/problem/11286 11286번: 절댓값 힙 첫째 줄에 연산의 개수 N(1≤N≤100,000)이 주어진다. 다음 N개의 줄에는 연산에 대한 정보를 나타내는 정수 x가 주어진다. 만약 x가 0이 아니라면 배열
l1m3kun.tistory.com
'Algorithm > 개념' 카테고리의 다른 글
| [알고리즘] 누적합(Prefix Sum) (0) | 2024.04.02 |
|---|---|
| [자료구조] 큐(Queue) (0) | 2024.03.12 |
| [알고리즘] 문자열 - 트라이(Trie) (0) | 2024.02.04 |
| 크루스칼(Kruskal) - 최소 신장 트리(MST) (1) | 2024.01.10 |
| [알고리즘] Union-Find (1) | 2024.01.07 |

